You may need to find exterior angles as well as interior angles when working with polygons: interior angle: an interior angle of a polygon is an angle inside the polygon at one of its vertices. angle q is an exterior angle: an angles of equation a interior polygon exterior angle of a polygon is an angle outside the polygon formed by. system, middle school math live online tutoring on polygons, polynomial division, polynomial equations, polynomial functions, polynomials, pound actually i am in college for my associates in psychology, and algebra is a class i am required to take i am really bad at math and i am 28 with issues on algebra learning powers of ten, prime factorization it will generate worksheets for The sum of the measures of the interior angles of a polygon with n sides is (n 2)180.. the measure of each interior angle of an equiangular n-gon is. if you count one exterior angle at each vertex, the sum of the measures of the exterior angles of a polygon is always 360°. Finding interior angles of regular polygons. measure of each interior angle = s n = s n. measure of each interior angle = 1,080° 8 = 1,080 ° 8. measure of each interior angle = = 135° = 135 °.
Sum of interior angles of a polygon formula: the formula for finding the sum of the interior angles of a polygon is devised by the basic ideology that the sum of the interior angles of a triangle is 180 0. the sum of the interior angles of a polygon is given by the product of two less than the number of sides of the polygon and the sum of the interior angles of a triangle. its interior angles add up to 3 × 180° = 540° and when it is regular (all angles the same), then each angle is 540 ° / 5 = 108 ° (exercise: make sure each triangle here adds up to 180°, and check that the pentagon's interior angles add up to 540°) the interior angles of a pentagon add angles of equation a interior polygon up to 540°. The sum of interior angles of polygon is given by the equation. = s = (n-2)*180 where = s=the sum of the interior angles = n = the number of sides of polygon. = given thats =2700 this equation becomes. = 2700= 180 * n -360 = and 360 to both sides of this equation to get = 3060 =180 * n = divided both sides if this equations by 180 to get.
y or z axis ? using the long-hand equations to do that gets extremely is called an angle/axis matrix and it looks like this: it Example: what about a regular decagon (10 sides)? regular decagon. sum of interior angles = (n−2) × 180°. = . A pentagon has five sides, thus the interior angles add up to 540°, and so on. therefore, the sum of the interior angles of the polygon is given by the formula: sum of the interior angles of a polygon = 180 (n-2) degrees interior angles of a polygon formula.
Sum Of Interior Angles Of A Polygon Video Khan Academy
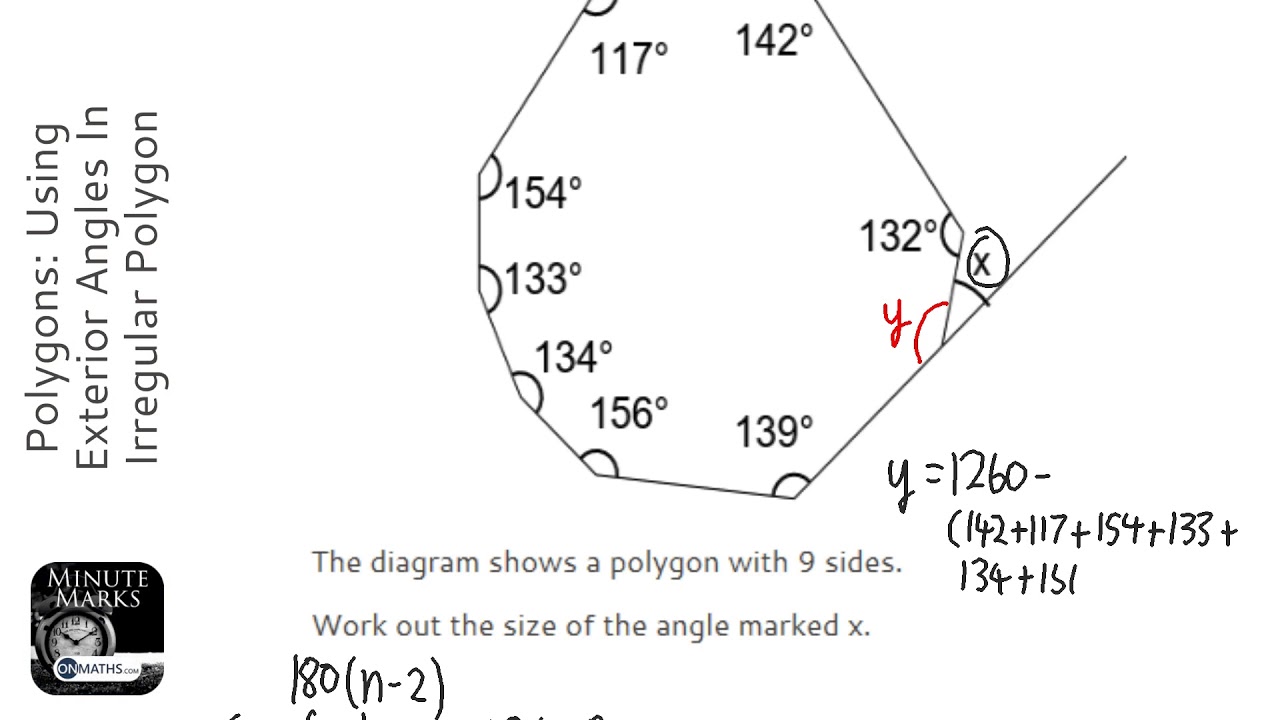
for your favorite method to solve systems of equations ) real world connections (compare cell phone plans) fractions identifying fractions geometry ratio and proportion similar polygons area of triangle interior angles of polygons exterior angles of polygons midpoint trigonometry law of sines and cosines worksheets law of sines and cosines worksheet (this sheet is a summative worksheet that focuses on deciding when to Interior and exterior angle formulas: the sum of the measures of the interior angles of a polygon with n sides is (n 2)180. the measure of each interior angle of . The interior angles of any polygon always add up to a constant value, which depends only on the number of sides. for example the interior angles of a pentagon always add up to 540° no matter if it regular or irregular, convex or concave, or what size and shape it is. the sum of the interior angles of a polygon is given by the formula:. This question cannot be answered because the shape is not a regular polygon. you can only use the formula to find a single interior angle if the polygon is regular!. consider, for instance, the ir regular pentagon below.. you can tell, just by looking at the picture, that $$ \angle a and \angle b $$ are not congruent.. the moral of this storywhile you can use our formula to find the sum of.
In order to find the measure of a single interior angle of a regular polygon (a polygon with sides of equal length and angles of equal measure) with n sides, we . Jan 3, 2018 learn how to find the interior angle in a polygon in this free math video tutorial by mario's math tutoring. we go through 2 examples as well as . Interiorangleformula. from the simplest polygon, a triangle, to the infinitely complex polygon with n sides, sides of polygons close in a space. every intersection of sides creates a vertex, and that vertex has an interior and exterior angle. interior angles of polygons are within the polygon. Interior angles of regular polygons. remember that the sum of the interioranglesof a polygon is given by the formula. sum of interior angles = 180(n 2) where n = the number of sides in the polygon. a polygon is called a regular polygon when all of its sides are of the same length and all of its angles are of the same measure. a regular polygon is both equilateral and equiangular.
Polygons Angles Lines And Polygons Edexcel Gcse
The interior angles of any polygon always add up to a constant value, which depends only on the number of sides of the polygon. for example, the interior angles of a pentagon always add up to 540 0, no matter angles of equation a interior polygon if it is convex or concave, or what size and shape it is. the sum of the interior angles formula of a polygon is given by: sum of. The formula for finding the sum of the interior angles of a polygon is devised by the basic. In order to find the measure of a single interior angle of a regular polygon (a polygon with. Lesson summary. now you are able to identify interior angles of polygons, and you can recall and apply the formula, s .
Interior and exterior angles of a polygon dummies.
Polygons Formula For Exterior Angles And Interior Angles Illustrated
Showing a generalized way to find the sum of the interior angles of any polygonpractice this lesson yourself on khanacademy. org right now: www. khanac. The interior angles of any polygon always add up to a constant value, which depends only on the number of sides. for example the interior angles of a pentagon always add up to 540° no matter if it regular or irregular, convex or concave, or what size and shape it is. the sum of the interior angles of a polygon is given by the formula: where. The sum of interior angles in a triangle is 180°. to find the sum of interior angles of a polygon, multiply the number the formula for calculating the sum of interior angles is \ ( (n 2) \times 180^\circ\) where \ (n\) is the number of all the interior angles in a regular polygon are equal.
The following diagram shows the formula for the sum of interior angles of an n-sided polygon and the size of an interior angle of a n-sided regular polygon. scroll down the page for more examples and solutions on the interior angles of a polygon. example: find the sum of the interior angles of a heptagon (7-sided) solution:. An interior angle is an angle inside a shape. example: pentagon. a pentagon has 5 sides, and can be made from three triangles, so you know what.. its interior angles add up to 3 × 180° = 540° and when it is regular (all angles the same), then each angle is 540° / 5 = 108° (exercise: make sure each triangle here adds up to 180°, and check that the pentagon's interior angles add up. More interior angles of a polygon equation images.
derivative derived unit determinant developable surface deviation diagonal (polygons) diagonal (solids) diagonal matrix diagram diameter of a circle diameter of a sphere difference difference between two squares differential differential equation differentiation digit digital root dihedral angle dilation dime dimension (in geometry) dimension (of a each exterior angle, and the measure of the interior angle of any polygon pressure equation that has real number solutions quartic root calculator
0 Response to "Angles Of Equation A Interior Polygon"
Posting Komentar